Positive and negative numbers are like the two sides of a coin in math. They help us understand amounts above and below zero. This lesson breaks down these numbers in a simple, fun way so students can easily grasp how they work and use them in real life, like tracking money or checking the weather.
Lesson Objectives
At the end of this entire lesson of mathematics of positive and negative numbers, you will:
- Understand what positive and negative numbers are.
- Spot them on a number line.
- Add, subtract, multiply, and divide them with confidence.
- Use them in everyday situations like money or temperature.
- Test your skills with an MCQ quiz on positive and negative numbers from every angle and ace it with confidence
What Are Positive and Negative Numbers?
Definitions Made Simple
- Positive Numbers: These are numbers bigger than zero, like 1, 5, or 10.5. You might see them with a “+” sign (e.g., +3) or no sign at all.
- Negative Numbers: These are numbers smaller than zero, like -1, -5, or -10.5. They always have a “−” sign.
- Zero: This is the middle point. It’s neither positive nor negative.
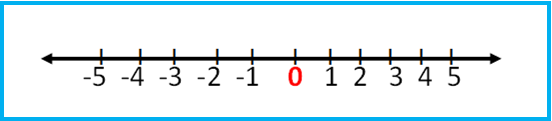
The Number Line
Think of a number line as a ruler that stretches left and right from zero:
- Numbers to the right of zero are positive (e.g., 1, 2, 3).
- Numbers to the left of zero are negative (e.g., -1, -2, -3).
- The farther a number is from zero, the bigger its absolute value (how far it is from zero, always a positive number).
Example Number Line:
Activity 1: Try It Out
- Draw a number line from -6 to 6.
- Plot these numbers: -3, 2, -5, 0, 4.
- Ask yourself and answer the questions: Which are positive? Which are negative? How far is each from zero?
Where Do We See Positive and Negative Numbers?
These numbers pop up in everyday life and here are some of them:
- Temperature: 10°C is warm (positive), but -5°C is chilly (negative).
- Money: Earning $20 is positive (+20), but owing $15 is negative (-15).
- Elevation: 100 meters above sea level is positive (+100), but 50 meters below is negative (-50).
- Time: 2 years from now is positive (+2), but 3 years ago is negative (-3).
Activity 2: The followings are some real-Life Scenarios
Match these situations to positive or negative numbers:
- A submarine dives 200 meters below sea level.
- You have deposited $50 in your bank account.
- The temperature is -8°C this morning.
- A hiker climbs 300 feet up a hill.
Do this assignment: Write the number with its sign (+ or -) for each and explain why.
Doing Math with Positive and Negative Numbers
Adding Numbers
Adding numbers is like moving on the number line in either way:
- Positive + Positive: Move right. Example: 3 + 2 = 5. You moved 2 steps to the right
- Negative + Negative: Move left. Example: -3 + (-2) = -5. You moved 2 steps to the left
- Positive + Negative: The answer depends on which number is “stronger” (has a bigger absolute value).
Easy Rule for Positive + Negative:
- Find the absolute value of each number (ignore the sign). For example, |-7| = 7, |4| = 4.
- Subtract the smaller absolute value from the larger one.
- Use the sign of the number with the bigger absolute value.
Examples:
- -7 + 4:
- Absolute values: |-7| = 7, |4| = 4.
- Subtract: 7 – 4 = 3.
- Sign: Negative (because 7 > 4 and -7 is negative). Answer: -3.
- 6 + (-2):
- Absolute values: |6| = 6, |-2| = 2.
- Subtract: 6 – 2 = 4.
- Sign: Positive (because 6 > 2). Answer: 4.
Number Line Trick:
- For -7 + 4, start at -7, move 4 steps right, land at -3.
- For 6 + (-2), start at 6, move 2 steps left, land at 4.
Try Solving 8 + (-5). Check your answer with the number line.
Subtracting Numbers
Subtraction is just adding the opposite. For example, 5 − 2 is the same as 5 + (-2). The opposite of a positive number is negative, and the opposite of a negative number is positive.
Steps to take:
- Rewrite the subtraction as addition of the opposite.
- Use the addition rules from above.
Examples for All Cases:
- Positive − Positive: 6 − 4 = 6 + (-4) = 2 (start at 6, move 4 left).
- Negative − Negative: -6 − (-4) = -6 + 4 = -2 (start at -6, move 4 right).
- Positive − Negative: 5 − (-3) = 5 + 3 = 8 (both positive, just add).
- Negative − Positive: -5 − 3 = -5 + (-3) = -8 (both negative, add absolute values and keep the negative sign).
Number Line Trick:
- For 6 − 4, start at 6, move 4 left to 2.
- For -6 − (-4), start at -6, move 4 right to -2.
- For 5 − (-3), start at 5, move 3 right to 8.
- For -5 − 3, start at -5, move 3 left to -8.
Try It: Solve -8 − 2. Rewrite it, solve, and check with the number line.
Multiplying and Dividing Numbers
Multiplying and dividing positive and negative numbers is all about the signs:
- Same Signs = Positive:
- Positive × Positive: 3 × 2 = 6.
- Negative × Negative: -3 × -2 = 6.
- Different Signs = Negative:
- Positive × Negative: 3 × -2 = -6.
- Negative × Positive: -3 × 2 = -6.
Division works the same way:
- -8 ÷ 2 = -4 (different signs, negative).
- -8 ÷ -2 = 4 (same signs, positive).
Activity 3: Practice Time
Solve these and explain the sign:
- -4 + 6
- 7 − (-2)
- -3 × 5
- -12 ÷ -3
Understanding Absolute Value
The absolute value of a number is how far it is from zero on the number line. It’s always positive or zero.
- Notation: |x|. Examples: |-5| = 5, |3| = 3.
- It ignores the sign, focusing only on distance.
Example:
Solve |−7 + 2|.
- First, do the math inside: -7 + 2 = -5.
- Then, find the absolute value: |-5| = 5.
Activity 4: Try Absolute Value
Find the absolute value for:
- |-8|
- |3 − 7|
- |-2 + (-4)|
Answer: Why are the answers always positive or zero?
Using Positive and Negative Numbers in Real Life
These numbers help solve real-world problems like tracking money, measuring temperature, or finding elevation.
Example Problem:
A submarine is 50 meters below sea level (-50 m). It rises 20 meters, then dives 30 meters. What’s its final depth?
- Start: -50.
- Rise 20: -50 + 20 = -30.
- Dive 30: -30 + (-30) = -60.
- Answer: -60 meters (60 meters below sea level).
Activity 5: Solve These Problems
- Your bank account has $100. You withdraw $150, then deposit $75. What’s the balance?
- The temperature is -10°C. It rises 15°C, then drops 5°C. What’s the final temperature?
- A stock changes by -2 points, +5 points, then -3 points. What’s the total change?
Key Points You Have Learned
- Positive numbers are above zero; negative numbers are below zero.
- Use a number line to see where numbers are and how they move when adding or subtracting.
- For multiplication and division, same signs give positive, different signs give negative.
- Absolute value is the distance from zero, always positive or zero.
- These numbers are used in real life for things like money, temperature, and elevation.

